Mathfoundation in Applied Cryptography

数论基础

数论是研究整数性质的一个数学分支，是密码学的基础学科之一。

素数与互素

“|” : 整除符号，a|b表示a是b的除数（或因子），b是a的倍数

素数 : 大于1的整数p只被1或它本身整除，则p被称为素数（或质数）

定理1 : 若p是素数，a是任意整数，则有p|a或(p,a)=1 . 即素数与一个数要么互素，要么可整除该数. (p,a)=1 表示互素（只有一个公因数“1”）

定理2 : 若p是素数，p|ab,则p|a或p|b，公因子:整数a能整除整数a₁,a₂,a₃…a_n，则称a为这几个整数的公因子，最大公因子记作gcd(a₁,a₂,a₃…a_n)或(a₁,a₂,a₃…a_n);若最大公因子为1，则称这几个整数互素

定理3 : 设a,b,c是任意不为零的整数，且
a=qb+c;其中q是整数
则有 gcd(a,b)=gcd(b,c)
即被除数和除数的最大公因子与除数和余数最大公因子相同.
例如 ：
gcd(18,12)=gcd(12,6)=gcd(6,0)=6
gcd(11,10)=gcd(10,1)=gcd(1,9)=1

欧几里得算法

欧几里得算法也被称为辗转相除法

任给两个整数a和b，不失一般性可假设a>b>0,由带余数的除法（简称带余除法），有下列等式:

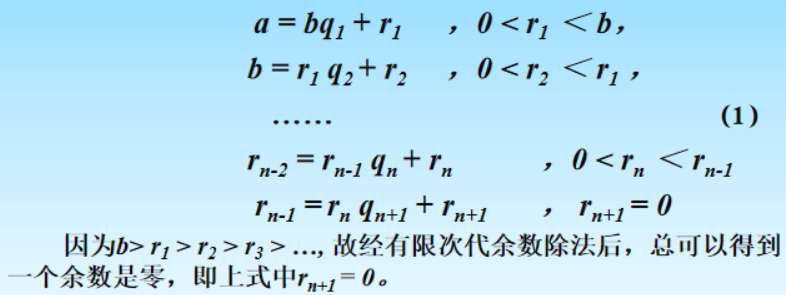
定理4 : 任给整数a>b>0,则最大公因子gcd(a,b)就是式(1)中的最后一个不等于零的余数，即gcd(a,b)=r_n

定理5 : 任给整数a>b>0,则存在两个整数m和n使得

由上式，显然有推论:a和b的公因数是gcd(a,b)的因数

例题 :

模运算与同余式

用辗转相除法求乘法逆元 :

其中550为550的乘法逆元

费马定理与欧拉定理

费马定理

定理6 : p是素数，a是与p互素的正整数，则

显然有: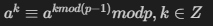

即为拆分，例如利用费马定理计算

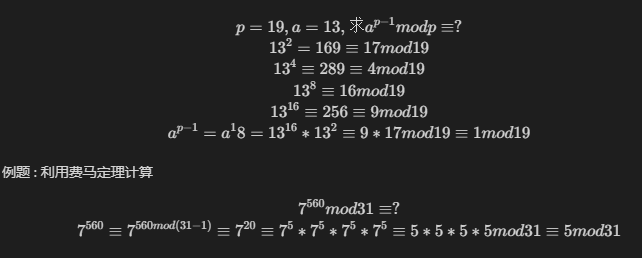
欧拉函数

欧拉定理

中国剩余定理

又称”孙子定理”，通过中国剩余定理可以由两两互素的整数对某数取模得到的余数求解该数

李永乐老师讲解中国剩余定理

三人同行七十稀
五树梅花二十一
七子团圆正半月
减百零五便得知

70a+21b+15c-105n=x

help: 有没有大佬知道为什么我vscode中写的这个markdown文件中，用了LaTeX语法，在这里预览的是成功显示出了数学符号之类的，但是在用hexo上传至github之后就显示不出来，而是全显示成了$$语句$$的样子，求助求助，是不是未能识别到LaTeX语法呀？如何解决QAQ